INDEX Back to Main Fire Control Page
A. Fire Control Problem
B. Basic elements of lead-computing sights
C. Gun sight Mark 15
D. Gun Fire Control System Mark 63
E. Gun Fire Control System Mark 56, Page 1 (This Page)
E. Gun Fire Control System Mark 56, Page 2
E. Gun Fire Control System Mark 56, Page 3
E. Gun Fire Control System Mark 56, Page 4
E. Gun Fire Control System Mark 56, Page 5
E. Gun Fire Control System Mk 56, Pg 1
E. Gun Fire Control System Mark 56 26E1.
General Gun Fire Control System Mark 56, like other ordnance equipment, is constantly being improved. Thus the following discussion may not reflect current installations in every detail. General operating principles of Mark 56 systems are the same for all equipment; but the latest publications, instructions, and notices should be consulted.
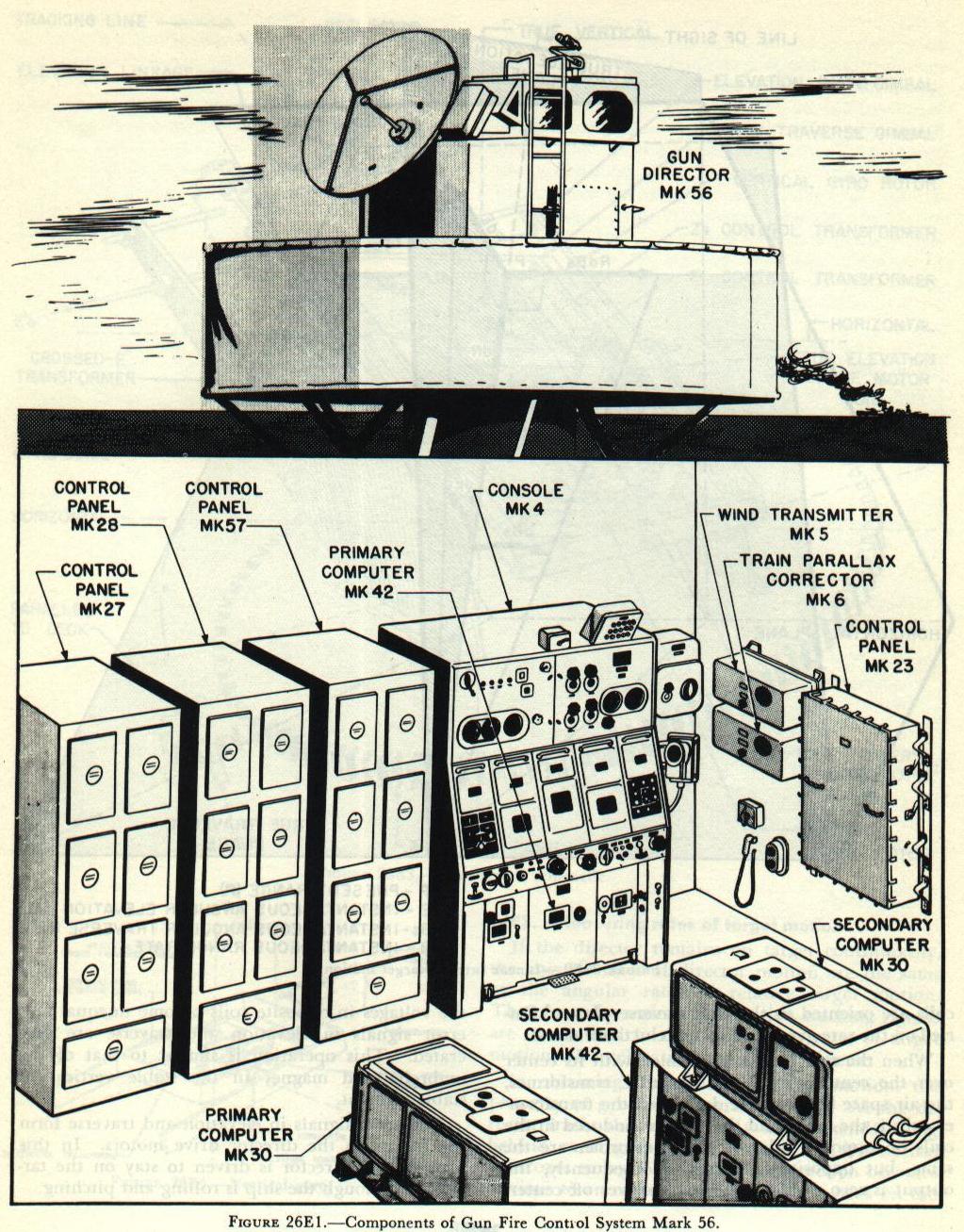
Gun Fire Control System Mark 56, illustrated in
figure 26E1, is an intermediate-range antiaircraft fire control system. Designed for use against high-speed subsonic aircraft targets, it provides gun train, gun elevation, and fuze orders for 3-, 5- and 6-inch guns. It may also be used against surface targets. Where a ship has two batteries (of different calibers) capable of AA fire, the system can produce different gun orders for both batteries simultaneously, thus permitting both to fire on the same target. This variation is known as a dual-ballistic system.
The system incorporates:
1. Automatic radar tracking in bearing, elevation, and range, as accurate as the best optical tracking.
2. Remote control of the entire system from the control room below decks, which provides for rapid radar acquisition of obscured targets and for blind firing. Solution time of this system is relatively short (2 seconds), so firing can begin early in tracking.
The system consists essentially of a two-axis, power-driven, direct-line-of-sight director located above decks, and various computing units located in a control room below decks. Complete radar equipment is included as an integral part of the system. The radar antenna is mounted on the director, and all radar indicators are in the control room.
The system is operated by a crew of four men, including the control officer. The latter and the pointer are stationed in the director for optical acquisition and the tracking of visible targets, and the two other men are at a console in the control room. On the console are all radar indicators and operational controls for handling range and positioning the director. Acquisition of obscured targets is accomplished from the console by matching designating dials.
Director line of sight (including radar antenna) is stabilized by a gyro unit in the director. Computation of lead angles is based on director angular rates of motion in stabilized coordinates. The discussion to follow presents first a general treatment of the fire control problem as solved by the system, then a detailed description of system components and operational controls.
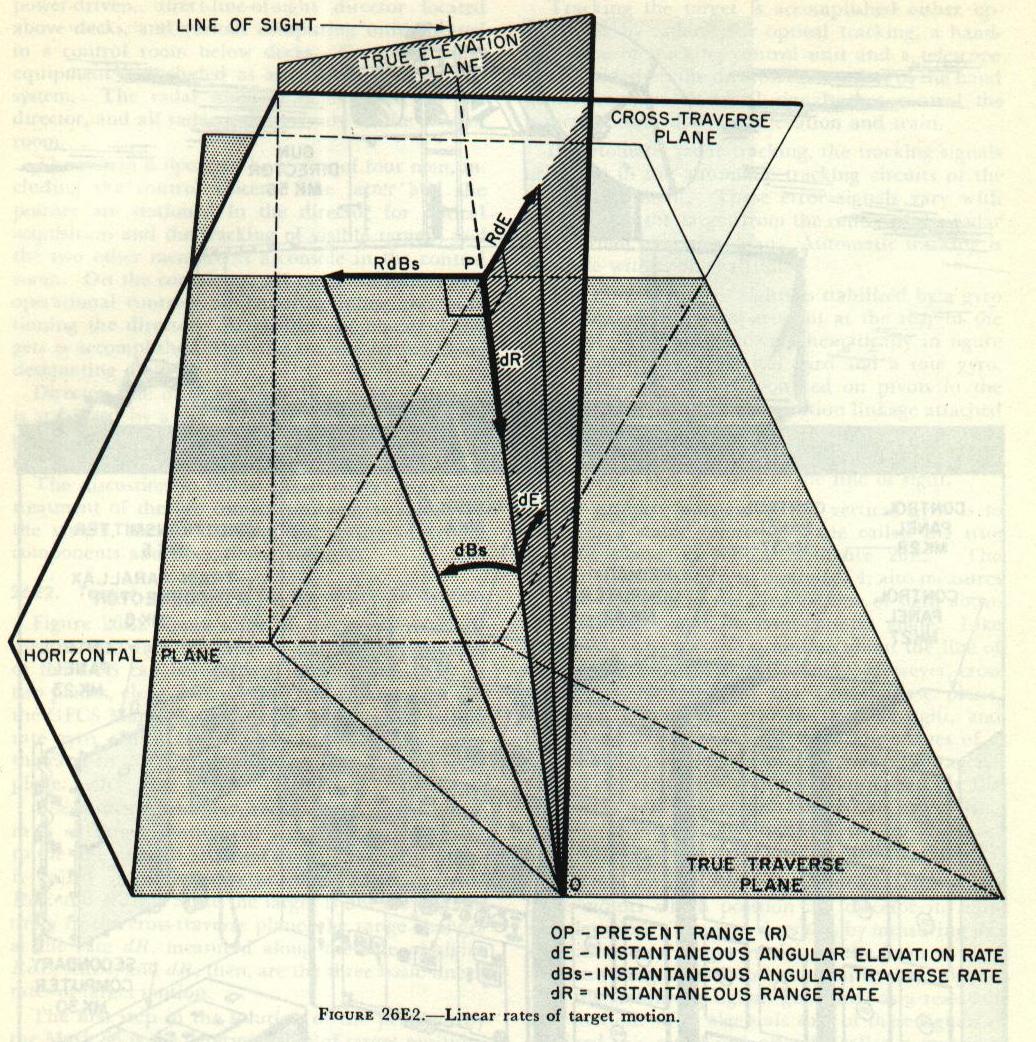 Figure 26E2
Figure 26E2 shows some of the space relations used in the Mark 56 system. The angular velocity of the LOS can be resolved into angular rates in two planes, elevation and traverse, dE and dBs. In the GFCS Mark 56, these rates are measured by the rate gyro, which is stabilized and hence measures the rates in the true elevation and the true traverse plane.
The solution, however, requires the use of linear rates of target motion, in a plane perpendicular to the line of sight at target’s position. This plane is called the cross-traverse plane, and contains RdE and RdBs. Since the target is not moving entirely in the cross-traverse plane, the range changes at the rate dR, measured along the line of sight. RdE, RdBs, and dR, then, are the three basic linear rates of target motion.
The first step in the solution of the problem by the Mark 56 is the determination of target position. Target bearing and elevation are measured by the director. As the target is tracked, director train, B’r’ and director elevation E’b are measured and transmitted by the synchros; electrical signals representing these angles are transmitted continuously to the computer. Target range (R) is measured by gating the target pip on the radar indicator. The range signal is transmitted automatically from the radar equipment to the computer.
Tracking the target is accomplished either optically or by radar. For optical tracking, a handgrip type of tracking control unit and a telescope are provided on the director. Rotation of the hand grips generates electrical signals that control the director power drives in elevation and train.
In automatic radar tracking, the tracking signals originate in the automatic tracking circuits of the radar equipment. These error signals vary with deviation of the target from the (enter of the radar beam when in conical scan. Automatic tracking is accurate within one-half mile.
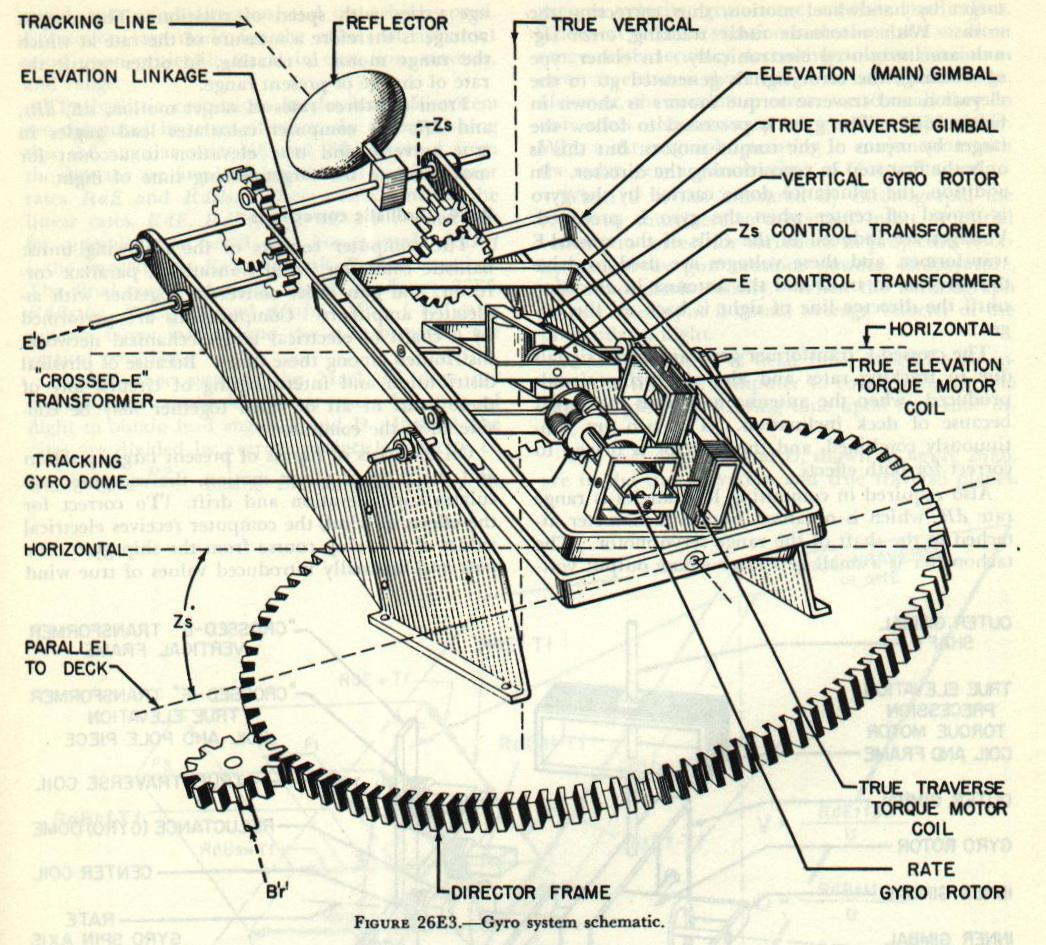
The director line of sights is stabilized by a gyro unit, located in a compartment at the rear of the director. The unit, shown schematically in
figure 26E3, consists of a vertical gyro and a rate gyro. The gyroscope unit is mounted on pivots in the gyro compartment. The elevation linkage attached to the antenna elevating gear is used to tilt the gyro main (elevation) gimbal so as to maintain the gyro gimbal axes parallel to the line of sight.
The primary purpose of the vertical gyro is to
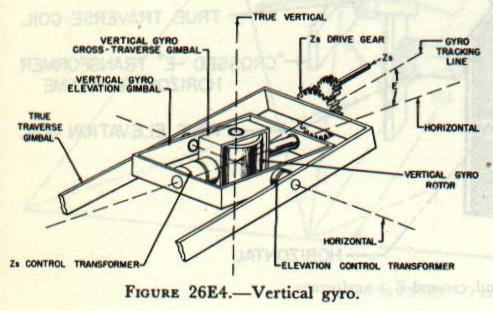
establish a stable reference plane called the true traverse plane, as shown in
figure 26E2. The vertical gyro, as shown in
figure 26E4, also measures E, true elevation of the director line of sight above the horizontal, and Zs, cross-traverse angle. Like cross level, cross traverse is motion about the line of sight due to movement of the deck. However, cross traverse is measured in the cross-traverse plane, which is perpendicular to the line of sight, and therefore differs from cross level. The values of E and Zs are picked off by elevation and cross-traverse control transformers and are transmitted to the computer, where they are applied in calculating ballistic corrections and gun orders. Zs also goes to the cross-traverse drive gear of the rate gyro.
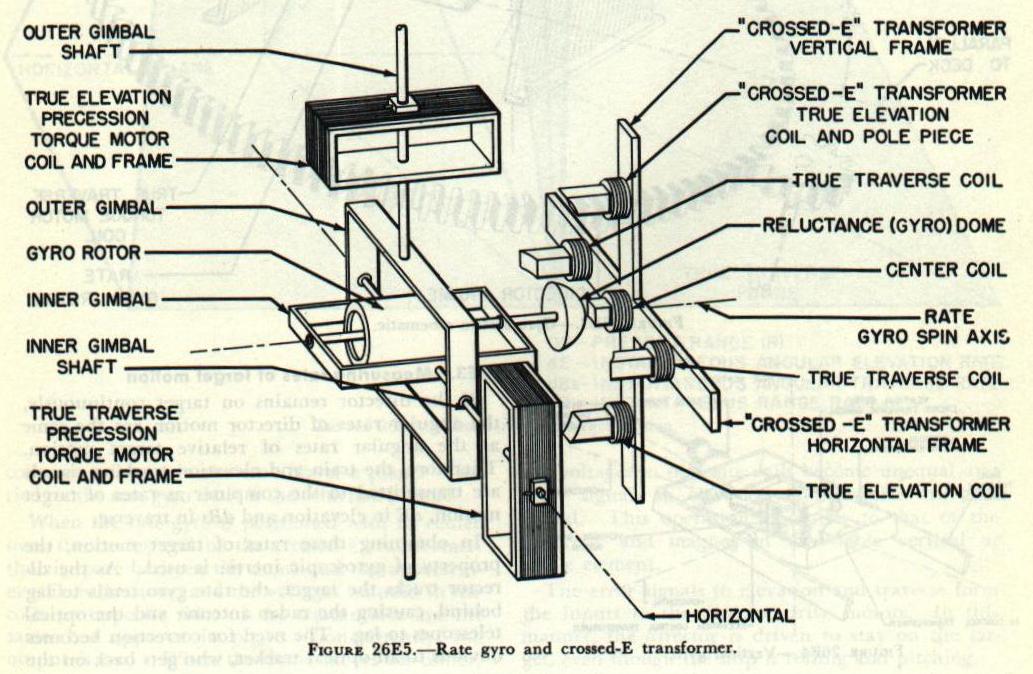
The rate gyro, shown in
figure 26E5, controls the drive motors which position the director in train and elevation. The gyro does this by measuring the angular rates of target motion in the form of electrical tracking signals and combining these signals with the stabilizing signals generated as a result o deck motion. The algebraic sum of these signals is obtained in a set of pick-off coils called a crossed-E transformer and shown in
figure 26E5. The crossed-E transformer is composed of five coils arranged to form a cross with axes at right angles. The center coil is energized by 100 volts, alternating current. This voltage induces voltages in the other coils. Supported by the vertical frame, coils are kept oriented in the vertical plane through the tracking line, as shown in
figure 26E3, and are connected in phase opposition. The other two coils are oriented in the true traverse plane. Carried on the rate gyro shaft is the reluctance dome.
When the rate gyro is positioned with its center over the center coil of the crossed-E transformer, the air space between the dome and the transformer coils is the same, and the voltages induced in the coils on opposite sides of the transformer are the same, but opposite in phase. Consequently, the output is zero. When the dome moves off center,
the voltages in opposite coils become unequal and error signals in elevation and traverse are generated. This operation is similar to that of the umbrella and magnet in the stable vertical or stable element.
The error signals in elevation and traverse form the inputs to the director drive motors. In this manner, the director is driven to stay on the target, even though the ship is rolling and pitching.
26E3. Measuring rates of target motion
If the director remains on target continuously, the angular rates of director motion are the same as the angular rates of relative target motion.
Therefore, the train and elevation tracking signals are transmitted to the computer as rates of target motion, dE in elevation and dBs in traverse.
In obtaining these rates of target motion, the property of gyroscopic inertia is used. As the director tracks the target, the rate gyro tends to lag behind, causing the radar antenna and the optical telescopes to lag. The need for correction becomes obvious to an optical tracker, who gets back on the target by handwheel motion, thus correcting the error. With automatic radar tracking, error signals are introduced electronically. In either type of tracking, the error signals generated go to the elevation and traverse torque motors as shown in
figure 26E5. The gyro is precessed to follow the target by means of the torque motors, but this is only the first step in repositioning the director. In addition, the reluctance dome carried by the gyro is moved off center when the gyro is precessed. Voltages arc induced in the coils of
the crossed-E transformer, and these voltages are used to drive the director in train and the antenna in elevation until the director line of sight is back on the target.
The crossed-E transformer generates error signals due to tracking rates and also stabilizing signals produced when the antenna moves off the target because of deck inclination. The two are continuously combined, and the director is driven to correct for both effects.
Also required in computing lead angles is range rate dR, which is obtained from a tachometer attached to the shaft of the range rate servo motor. The tachometer is a small generator whose output voltage varies with speed of rotation. The output voltage is therefore a measure of the rate at which the range motor is rotating, in other words the rate of change of present range.
From the three rates of target motion, dE, dBs, and dR, the computer calculates lead angles in true traverse and true elevation to account for movement of the target during time of flight.
Bottom of Page 1
